Fraction Decomposition Calculator
Fractions are one of the foundational building blocks of math. From elementary school to advanced calculus, understanding how to work with fractions is essential for success in almost every area of math. But it’s not just about adding or subtracting them—it’s about seeing how numbers can be broken down, reassembled, and analyzed more flexibly.
Imagine trying to solve a complex equation or integrate a function in calculus without being able to break the fraction into simpler parts. It’s like trying to solve a puzzle without first separating the pieces. Fractions are everywhere—in ratios, proportions, measurements, algebraic expressions, and even probability.
Understanding fractions helps students:
- Develop a deeper understanding of number relationships
- Understand the logic behind equations and functions
- Prepare for higher-level topics like rational expressions, limits, and integers
This is where fraction decomposition comes in. It’s a powerful method used to simplify rational expressions, making them easier to work with, especially in algebra and calculus. And now, thanks to tools like fraction decomposition calculators, this process can be done in seconds – but only if you understand the math behind it.
How to Use ? Fraction Decomposition calculator.
Fill the Follow column
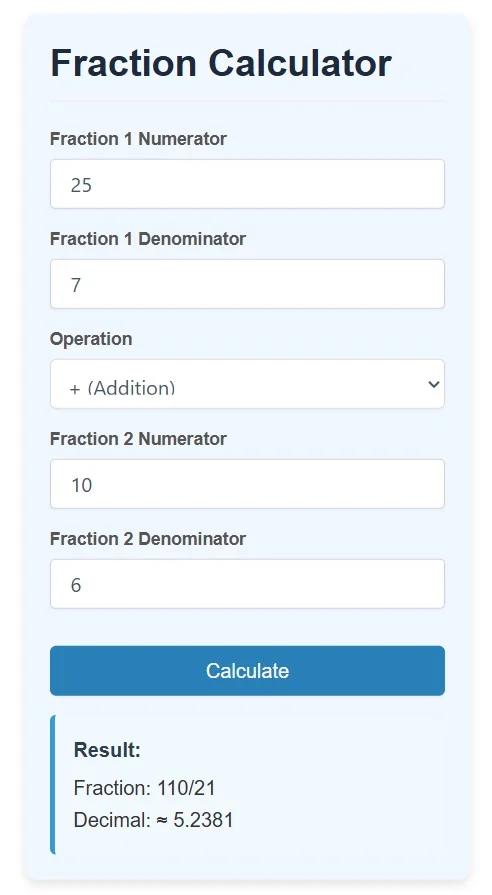
Apply on Calculate button
Result saw in Fraction & Decimal
🔹 A brief mention of the struggle with complex rational expressions
As students progress in mathematics, they inevitably encounter rational expressions – fractions where the numerator and/or denominator contain polynomials. At first glance, these expressions seem daunting. Unlike simple numerical fractions, rational expressions involve variables, exponents, and often complex factorization.
For example, take something like this:
(3 𝑥 + 5)/ ( 𝑥 − 2 ) ( 𝑥 + 1 )
It’s not immediately obvious how to work with this type of expression, especially when it comes to:
- Simplifying the expression
- Solving equations
- Iintegrating in calculations
- Qr simply understanding the structure of the function
Many students struggle at this stage because rational expressions require a strong understanding of algebraic manipulations – factoring, common denominators and substitutions – all layered on top of each other. It’s easy to make small mistakes that throw off the entire problem.
That’s why fraction decomposition is a valuable technique. It breaks a complex rational expression into simpler, more digestible pieces – turning a complex fraction into simpler pieces. But even decomposition can be challenging to do by hand.
This is where the Fraction Decomposition Calculator comes in handy. It takes the heavy lifting out of your work and allows you to focus on understanding the steps and logic behind the breakdown – without getting bogged down in algebraic frustration. Do you want to continue building the post one section at a time, or do you want a full draft next?
🔹 Introducing the Tool: Fraction Decomposition Calculator
Now that we’ve touched on how difficult complex rational expressions can be, let’s introduce a tool that can make working with them a lot easier: a fraction decomposition calculator.
A fraction decomposition calculator is an online or software-based tool that helps break rational expressions into partial fractions – simpler components that are easier to analyze, integrate, or simplify.
Instead of manually going through steps like factoring the denominator, setting up equations for unknown constants, and solving them (which can be time-consuming and error-prone), the calculator handles it all right away. All you need to do is:
- Enter your rational expression (e.g. (e.g., 3x + 5 / (x² – x – 2))
- Let the calculator do the work
- Get the partial fraction form (e.g., A/(x-2) + B/(x+1))
This tool is especially useful for:
- Students learning algebra or calculus
- Teachers wanting to demonstrate fraction decomposition in class
- Anyone working on problems involving the integration of rational functions
Best of all, many of these calculators are free, browser-based, and don’t require a download. They’re designed to give you fast, accurate results – and often even show you a step-by-step process, which helps reinforce learning. In the next section, we’ll explore how these calculators work behind the scenes – so you can understand what’s going on behind the scenes, not just take the answer at face value.
2. What is Fraction Decomposition ?
🔹 Preview what this post will cover
In this post, we’ll explore everything you need to know about fraction decomposition calculators – not just what they are, but how they work and why they’re so useful.
Here’s what you can expect as you read:
A clear explanation of what fraction decomposition means and why it’s important in algebra and calculus.
An in-depth look at the fraction decomposition calculator – what it does, how it processes complex rational expressions, and how it saves time.
A step-by-step breakdown of how the calculator works, so you can understand the logic behind the results.
A real-world example, showing how a complex rational expression is converted to a partial fraction using a tool.
The advantages and limitations of doing it manually over using a calculator. Recommendations on where to find a good fraction decomposition calculator online.
By the end of this article, you will not only understand what a fraction decomposition calculator is, but you will also feel confident using it – whether you are checking your homework, solving an integration problem, or just trying to get a better grip on algebraic expressions.
✅ Definition:
Fractional decomposition — also known as partial fraction decomposition — is a method in algebra and calculus used to break down a complex rational expression (a fraction made up of polynomials) into a sum of simpler fractions.
Instead of working with a complex fraction like: 3 𝑥 + 5 ( 𝑥 − 2 ) ( 𝑥 + 1 ) (x−2)(x+1) 3x+5 ,
we rewrite it as a sum of smaller, more manageable fractions like: 𝐴 𝑥 − 2 + 𝐵 𝑥 + 1 x−2 A + x+1 B
Here, A and B are the constants we are solving for.
🍕 Real-world analogy:
Think of it like breaking a pizza into pieces. It is difficult to eat an entire pizza (complex fraction) at once, but if you cut it into smaller pieces (partial fraction), it is much easier to manage. Or imagine you have a big task – you break it down into smaller tasks to make it easier to complete. Partial fraction decomposition does the same for large, messy algebraic fractions.
🧮 Why it’s used in math:
Fraction decomposition isn’t just a theoretical exercise – it’s extremely useful in real-world mathematical problems, especially when you’re dealing with:
Integration in calculus:
When integrating rational functions, it’s often impossible to integrate complex fractions directly. But once decomposed into partial fractions, each smaller piece fits into a standard integer form, which makes the overall problem much simpler.
Simplifying Algebraic Expressions:
In algebra, simplifying expressions using partial fractions can make it much easier to solve equations or understand the behavior of a function.
Solving Differential Equations:
Partial fractions often appear in methods like Laplace transforms, which are used in engineering and physics to solve complex differential equations.
Improving Conceptual Understanding:
It helps students understand the structure of rational expressions by showing how they are built from simpler components.
In short, fraction decomposition is a key technique that simplifies complex problems, uncovers hidden structure in equations, and makes life much easier when solving difficult math challenges – especially with the help of tools like fraction decomposition calculators.
Benefits of Using a Fraction Decomposition Calculato
A fraction decomposition calculator isn’t just a convenience – it’s a powerful tool that offers many practical benefits for both learning and problem solving. Here’s a breakdown of why using it can seriously improve your math workflow:
⏱️ 1. Saves time
One of the biggest benefits is speed. Manual partial fraction decomposition can involve several steps: Factoring polynomials Setting up the decomposition structure Solving systems of equations to find constants Combining and simplifying expressions Doing all of this by hand is time-consuming – especially if you’re working under pressure during homework, exams, or real-world applications. The calculator automates all of those steps in seconds, allowing you to move on to the next problem faster and with more confidence.
✅ 2. Reduces Errors
Let’s face it: Algebraic manipulation is tricky, and even a small mistake can ruin the entire solution. Common errors include: Incorrect factoring of the denominator Incorrectly setting the decomposition Arithmetic errors when solving for constants Fractional decomposition calculators handle all of this with absolute precision, ensuring that the decomposition is done correctly every time. This is especially helpful when you need a reliable answer quickly.
📚 3. Helps you learn and check homework
Many modern calculators don’t just give you the final answer – they also show you a step-by-step analysis. This is incredibly valuable to them: Students trying to understand the logic behind the method are checking your own manual work for errors Practicing the steps repeatedly until they click Instead of just copying the result, students can learn why each step is important, strengthening their understanding of algebraic principles.
👩🏫👨💻 4. Useful for both students and professionals
While students benefit from calculators in the learning environment, professionals in fields such as engineering, physics, or data science also use these tools when: Solving complex equations Analyzing system behavior Working with Laplace or Fourier transforms in control systems In professional settings, time is money – and accuracy is non-negotiable.
A calculator that can quickly and accurately simplify rational expressions is an asset in both academic and real-world situations.
In summary, the fraction decomposition calculator is more than just a math shortcut – it’s a reliable assistant that helps you work faster, reduce errors, strengthen your understanding, and complete tasks with confidence.
Limitations of Using a Fraction Decomposition Calculator
While the fraction decomposition calculator is incredibly useful, like any tool, it is not perfect – and it is important to be aware of its limitations. Understanding these shortcomings ensures that you are using the calculator wisely and effectively, not just blindly.
🧾 1. Dependence on correct input formatting This calculator is designed to read mathematical expressions in a specific way. If your input is not formatted correctly, the tool may:
Misinterpret your expression Return an error Give the wrong result
For example: Writing (x^2 + 3x + 2)/(x – 1) is usually fine,
But forgetting parentheses or using incorrect syntax like x^2 + 3x + 2/x – 1 can completely change the meaning
This means you need to be careful and precise when entering your expression – especially when working with complex polynomials or nested functions. Some calculators provide formatting assistance or built-in syntax checking, but not all do.
🧠 2. Doesn’t always teach the “why” behind the math
While a calculator gives you the correct result, it doesn’t always help you understand: Why we factor fractions in a particular way
How to solve for constants
What the factorization reveals about the structure of the function
In short, you may get an answer, but not insight.
This is especially important for students. If you rely solely on a calculator without learning the method, you may struggle during tests or in more advanced courses where tools are not allowed.
🎓 3. Best used as a supplement to learning, not a replacement
Fraction factoring calculators are best used as a learning aid – not as a scaffold. It’s great for:
Double-checking your manual work
Visualizing how a complex expression breaks down
Saving time on repetitive steps
Reinforcing your understanding after learning the basics
But it will never completely replace learning how partial fraction decomposition works. Mastering the underlying concepts will make you a stronger, more confident math student – and give you the flexibility to solve problems with or without technology.